[ AVL트리 ]
자가 균형 트리(편향 트리를 막아줌).
[ 전체 코드 ]
AVLTree.h
#pragma once
#include <assert.h>
template <typename Key, typename Value>
class CAVLTreeNode
{
template <typename Key, typename Value>
friend class CAVLTree;
template <typename Key, typename Value>
friend class CAVLTreeIterator;
private:
CAVLTreeNode() // 생성자.
{
m_pLeft = nullptr;
m_pRight = nullptr;
m_pParent = nullptr;
m_pNext = nullptr;
m_pPrev = nullptr;
}
~CAVLTreeNode() // 소멸자.
{
}
private:
CAVLTreeNode<Key, Value>* m_pLeft;
CAVLTreeNode<Key, Value>* m_pRight;
CAVLTreeNode<Key, Value>* m_pParent;
CAVLTreeNode<Key, Value>* m_pNext;
CAVLTreeNode<Key, Value>* m_pPrev;
public:
Key first;
Value second;
public:
// 디버깅용 출력함수.
void Output()
{
std::cout << "Key : " << first << " Value : " << second << std::endl;
std::cout << "Left : ";
if (!m_pLeft)
std::cout << "없음" << std::endl;
else
std::cout << m_pLeft->first << std::endl;
std::cout << "Right : ";
if (!m_pRight)
std::cout << "없음" << std::endl;
else
std::cout << m_pRight->first << std::endl;
std::cout << "Parent : ";
if (!m_pParent)
std::cout << "없음" << std::endl;
else
std::cout << m_pParent->first << std::endl;
std::cout << std::endl;
}
};
template <typename Key, typename Value>
class CAVLTreeIterator
{
template <typename Key, typename Value>
friend class CAVLTree;
public:
CAVLTreeIterator()
{
m_pNode = nullptr;
}
~CAVLTreeIterator()
{
}
private:
CAVLTreeNode<Key, Value>* m_pNode;
public:
bool operator == (const CAVLTreeIterator<Key, Value>& iter) const
{
return m_pNode == iter.m_pNode;
}
bool operator != (const CAVLTreeIterator<Key, Value>& iter) const
{
return m_pNode != iter.m_pNode;
}
void operator ++ ()
{
m_pNode = m_pNode->m_pNext;
}
void operator ++ (int)
{
m_pNode = m_pNode->m_pNext;
}
void operator -- ()
{
m_pNode = m_pNode->m_pPrev;
}
void operator -- (int)
{
m_pNode = m_pNode->m_pPrev;
}
CAVLTreeNode<Key, Value>* operator -> () const
{
return m_pNode;
}
};
template <typename Key, typename Value>
class CAVLTree
{
public:
CAVLTree()
{
m_pRoot = nullptr;
m_pBegin = new Node;
m_pEnd = new Node;
// begin과 end연결.
m_pBegin->m_pNext = m_pEnd;
m_pEnd->m_pPrev = m_pBegin;
m_iSize = 0;
}
~CAVLTree()
{
clear();
delete m_pBegin;
delete m_pEnd;
}
private:
typedef CAVLTreeNode<Key, Value> Node;
typedef CAVLTreeNode<Key, Value>* PNode;
public:
typedef CAVLTreeIterator<Key, Value> iterator;
private:
PNode m_pRoot;
PNode m_pBegin;
PNode m_pEnd;
int m_iSize;
public:
// 추가 (1. 반복문 이용 2. 재귀함숫 이용) >> 재귀함수 이용.
void insert(const Key& key, const Value& value)
{
if (!m_pRoot) // root가 null일 경우(처음 노드를 추가하는 경우)
{
m_pRoot = new Node; // root 생성.
m_pRoot->first = key; // ket 저장.
m_pRoot->second = value; // value 저장.
// root와 end를 연결.
m_pRoot->m_pNext = m_pEnd;
m_pEnd->m_pPrev = m_pRoot;
// root와 begin을 연결.
m_pRoot->m_pPrev = m_pBegin;
m_pBegin->m_pNext = m_pRoot;
}
else
{
PNode pNewNode = insert(key, value, m_pRoot);
}
++m_iSize;
}
// 크기.
int size() const
{
return m_iSize;
}
// 비어있는지 확인.
bool empty() const
{
return m_iSize == 0;
}
// 모두 지움.
void clear()
{
PNode pNode = m_pBegin->m_pNext; // begin의 다음 노드로 설정.
while (pNode != m_pEnd) // end가 아닐 동안 실행.
{
PNode pNext = pNode->m_pNext; // 지울 노드의 next를 저장.
delete pNode; // 지움.
pNode = pNext; // 지울 노드 바꿔줌.
}
// begin과 end 연결.
m_pBegin->m_pNext = m_pEnd;
m_pEnd->m_pPrev = m_pBegin;
m_iSize = 0;
m_pRoot = nullptr;
}
// 첫 노드 리턴.
iterator begin() const
{
iterator iter;
iter.m_pNode = m_pBegin->m_pNext;
return iter;
}
// 끝 노드 리턴.
iterator end() const
{
iterator iter;
iter.m_pNode = m_pEnd;
return iter;
}
// 찾기.
iterator find(const Key& key) const
{
assert(m_iSize != 0); // 노드가 존재하지 않는 경우, 경고창을 띄우고 종료 시킴.
return find(key, m_pRoot);
}
// 삭제.
iterator erase(const Key& key)
{
assert(m_iSize != 0); // 노드가 존재하지 않는 경우, 경고창을 띄우고 종료 시킴.
iterator iter = find(key, m_pRoot); // 지울 노드가 있는 지 확인.
if (iter.m_pNode == m_pEnd) // 지울 노드를 못 찼았을 경우.
return iter; // 그냥 리턴.
// 자식이 없는 노드일 경우, 그냥 지움.
if (!iter.m_pNode->m_pLeft && !iter.m_pNode->m_pRight) // left와 right가 없으면 자식 노드가 없다는 것을 의미.
{
PNode pNext = iter.m_pNode->m_pNext; // 지울 노드의 next 저장.
PNode pPrev = iter.m_pNode->m_pPrev; // 지울 노드의 previous 저장,
// 지울 노드의 next와 prevoius를 연결.
pPrev->m_pNext = pNext;
pNext->m_pPrev = pPrev;
if (!iter.m_pNode->m_pParent) // 부모 노드가 없을 경우.
m_pRoot = nullptr; // root를 null로 초기화.
else // 부모 노드가 있을 경우.
{
if (iter.m_pNode->m_pParent->m_pLeft == iter.m_pNode) // 지울 노드가 부모의 왼쪽 자식 노드일 경우.
iter.m_pNode->m_pParent->m_pLeft = nullptr; // 지울 노드 부모의 왼쪽 자식 노드를 null로 초기화.
else // 지울 노드가 부모의 오른쪽 자식 노드일 경우.
iter.m_pNode->m_pParent->m_pRight = nullptr; // 지울 노드 부모의 오른쪽 자식 노드를 null로 초기화.
}
PNode pParent = iter.m_pNode->m_pParent; // 기준 노드의 부모를 저장.
delete iter.m_pNode; // 노드 지움.
iter.m_pNode = pNext; // pNode를 지운 노드의 next로 지정.
--m_iSize;
ReBalance(pParent); // pParent를 중심으로 ReBalance.
return iter;
}
PNode pDeleteNode = nullptr; // 지울 노드.
bool bFindLeft = false;
if (iter.m_pNode->m_pLeft) // 지울 노드의 left가 있을 경우.
{
pDeleteNode = LeftMax(iter.m_pNode->m_pLeft); // LeftMax로 왼쪽에서 가장 큰 노드를 찾음.
bFindLeft = true;
}
else // 지울 노드의 right가 있을 경우.
{
pDeleteNode = RightMin(iter.m_pNode->m_pRight); // RightMin로 오른쪽에서 가장 작은 노드를 찾음.
}
// 지울 노드의 값으로 현재 노드를 대체.
iter.m_pNode->first = pDeleteNode->first;
iter.m_pNode->second = pDeleteNode->second;
// 지울 노드의 자식노드가 있을 경우 지울 노드의 자리를 대체.
if (bFindLeft) // 지울 노드가 왼쪽에 있을 경우.
{
if (pDeleteNode->m_pParent->m_pLeft == pDeleteNode) // 지울 노드가 부모의 왼쪽에 있을 경우.
pDeleteNode->m_pParent->m_pLeft = pDeleteNode->m_pLeft; // 지울 노드의 부모 노드와 지울 노드의 left를 연결. (지울 노드의 부모의 left를 지울 노드의 left로 설정.)
else // 지울 노드가 부모의 오른쪽에 있을 경우.
pDeleteNode->m_pParent->m_pRight = pDeleteNode->m_pLeft; // 지울 노드의 부모 노드와 지울 노드의 left를 연결. (지울 노드의 부모의 right를 지울 노드의 left로 설정.)
if (pDeleteNode->m_pLeft) // 지울 노드의 left가 있는 경우.
pDeleteNode->m_pLeft->m_pParent = pDeleteNode->m_pParent; // 지울 노드를 대체할 노드의 부모를 지울 노드의 부모와 연결. (지울 노드의 left의 부모를 지울 노드의 부모로 설정.)
}
else // 지울 노드가 오른쪽에 있을 경우.
{
if (pDeleteNode->m_pParent->m_pLeft == pDeleteNode) // 지울 노드가 부모의 왼쪽에 있을 경우.
pDeleteNode->m_pParent->m_pLeft = pDeleteNode->m_pRight; // 지울 노드의 부모 노드와 지울 노드의 right를 연결. (지울 노드의 부모의 left를 지울 노드의 right로 설정.)
else // 지울 노드가 부모의 오른쪽에 있을 경우.
pDeleteNode->m_pParent->m_pRight = pDeleteNode->m_pRight; // 지울 노드의 부모 노드와 지울 노드의 right를 연결. (지울 노드의 부모의 right를 지울 노드의 right로 설정.)
if (pDeleteNode->m_pRight) // 지울 노드의 right가 있는 경우.
pDeleteNode->m_pRight->m_pParent = pDeleteNode->m_pParent; // 지울 노드를 대체할 노드의 부모를 지울 노드의 부모와 연결. (지울 노드의 right의 부모를 지울 노드의 부모로 설정.)
}
PNode pNext = pDeleteNode->m_pNext; // 지울 노드의 next를 저장.
PNode pPrev = pDeleteNode->m_pPrev; // 지울 노드의 previous를 저장.
// 지울 노드의 next와 previous를 연결.
pNext->m_pPrev = pPrev;
pPrev->m_pNext = pNext;
if (bFindLeft) // 지울 노드가 왼쪽에 있을 경우.
iter.m_pNode = iter.m_pNode->m_pNext; // pNode를 pNode의 next로 설정.
else // 지울 노드가 오른쪽에 있을 경우.
iter.m_pNode = iter.m_pNode; // pNode를 pNode로 설정.
PNode pParent = pDeleteNode->m_pParent; // 삭제한 노드의 부모를 저장.
delete pDeleteNode; // 노드 지움.
--m_iSize;
ReBalance(pParent); // pParent를 중심으로 ReBalance.
return iter;
}
private:
PNode insert(const Key& key, const Value& value, PNode pNode)
{
// key값이 pNode(중심값)보다 작을 경우. 즉, 왼쪽에 배치하는 경우.
if (pNode->first >= key)
{
if (!pNode->m_pLeft) // 왼쪽 자식 노드가 없을 경우.
{
PNode pNewNode = new Node; // 새 노드 생성.
pNewNode->first = key; // key값 저장.
pNewNode->second = value; // value값 저장.
pNode->m_pLeft = pNewNode; // pNode의 left로 새 노드 설정.
pNewNode->m_pParent = pNode; // 새 노드의 부모로 pNode 설정.
PNode pPrev = pNode->m_pPrev; // 새 노드의 부모노드의 이전노드를 얻어옴.
pPrev->m_pNext = pNewNode; // 부모노드의 이전노드의 next를 새 노드로 설정.
pNewNode->m_pPrev = pPrev; // 새 노드의 previous를 부모노드의 이전노드로 설정.
pNewNode->m_pNext = pNode; // 새 노드의 next로 pNode 설정.
pNode->m_pPrev = pNewNode; // pNode의 previous로 새 노드 설정.
ReBalance(pNewNode); // 노드를 추가한 후에 밸런스가 맞추어져 있는지를 판단.
return pNewNode;
}
else // 자식 노드가 있을 경우
{
return insert(key, value, pNode->m_pLeft); // 기준 노드를 pNode의 left로 줌.
}
}
// 오른쪽에 배치할 경우
// 오른쪽 자식 노드가 없을 경우 오른쪽 자식으로 만들어준다.
if (!pNode->m_pRight)
{
PNode pNewNode = new Node; // 새 노드 생성.
pNewNode->first = key;// key값 저장.
pNewNode->second = value;// value값 저장.
pNode->m_pRight = pNewNode; // pNode의 right로 새 노드 설정.
pNewNode->m_pParent = pNode; // 새 노드의 부모로 pNode 설정.
PNode pNext = pNode->m_pNext; // 새 노드의 부모노드의 다음노드를 얻어옴.
pNext->m_pPrev = pNewNode; // 부모노드의 다음노드의 previous를 새 노드로 설정.
pNewNode->m_pNext = pNext; // 새 노드의 next를 부모노드의 다음노드로 설정.
pNewNode->m_pPrev = pNode; // 새 노드의 previous로 pNode 설정.
pNode->m_pNext = pNewNode;// pNode의 next로 새 노드 설정.
ReBalance(pNewNode); // 노드를 추가한 후에 밸런스가 맞추어져 있는지를 판단.
return pNewNode;
}
// 오른쪽 자식 노드가 있을 경우 오른쪽 자식노드를 넣어주어서 다시 탐색.
return insert(key, value, pNode->m_pRight);
}
iterator find(const Key& key, PNode pNode) const
{
if (!pNode) // 찾을 노드가 없을 경우
return end(); // end를 리턴.
else if (pNode->first == key) // 노드를 찾았을 경우.
{
iterator iter;
iter.m_pNode = pNode;
return iter;
}
if (pNode->first > key) // key값이 더 작을 경우, 왼쪽을 탐색.
return find(key, pNode->m_pLeft);
return find(key, pNode->m_pRight); // 아닐 경우, 오른쪽 탐색.
}
// 왼쪽에서 가장 큰 노드 찾기.
PNode LeftMax(PNode pNode)
{
if (!pNode->m_pRight) // 오른쪽 자식 노드가 없을 경우.
return pNode; // 현재 노드가 가장 큰 것이기 때문에 현재 노드를 리턴.
return LeftMax(pNode->m_pRight); // 아닐 경우. 오른쪽 노드를 기준으로 다시 찾음.
}
// 오른쪽에서 가장 작은 노드 찾기.
PNode RightMin(PNode pNode)
{
if (!pNode->m_pLeft) // 왼쪽 자식 노드가 없을 경우.
return pNode; // 현재 노드가 가장 작은 것이기 때문에 현재 노드를 리턴.
return RightMin(pNode->m_pLeft); // 아닐 경우. 왼쪽 노드를 기준으로 다시 찾음.
}
PNode RotationLeft(PNode pNode)
{
PNode pParent = pNode->m_pParent; // 부모노드를 얻음. 부모 노드가 있을 수도 있으므로
PNode pRight = pNode->m_pRight; // 기준노드의 오른쪽 자식을 얻음.
PNode pLeftChild = pRight->m_pLeft; // 기준 노드의 오른쪽 자식의 왼쪽 자식을 얻음.
pRight->m_pLeft = pNode; // pRight의 left를 기준 노드로 설정.
pNode->m_pRight = pLeftChild; // 기준 노드의 right를 pLeftChild로 설정.
if (pLeftChild) // pLeftChild가 있을 경우
pLeftChild->m_pParent = pNode; // pLeftChild의 부모를 기준 노드로 설정.
pRight->m_pParent = pParent; // pRight의 부모로 pParent로 설정.
if (pParent) // pParent가 있을 경우
{
if (pParent->m_pLeft == pNode) // pParent의 left가 기준 노드일 경우.
pParent->m_pLeft = pRight; // pParent의 left를 pRight으로 설정.
else // pParent의 right가 기준 노드일 경우.
pParent->m_pRight = pRight; // pParent의 right를 pRight으로 설정.
}
else // pParent가 없을 경우.
m_pRoot = pRight; // root를 pRight로 설정.
pNode->m_pParent = pRight; // 기준 노드의 부모를 pRight로 설정.
return pRight;
}
PNode RotationRight(PNode pNode)
{
PNode pParent = pNode->m_pParent; // 부모노드를 얻음. 부모 노드가 있을 수도 있으므로
PNode pLeft = pNode->m_pLeft; // 기준노드의 왼쪽 자식을 얻음.
PNode pRightChild = pLeft->m_pRight; // 기준 노드의 왼쪽 자식의 오른쪽 자식을 얻음.
pLeft->m_pRight = pNode; // pLeft의 right를 기준 노드로 설정.
pNode->m_pLeft = pRightChild; // 기준 노드의 left를 pRightChild로 설정.
if (pRightChild) // pRightChild가 있을 경우
pRightChild->m_pParent = pNode; // pRightChild의 부모를 기준 노드로 설정.
pLeft->m_pParent = pParent; // pLeft의 부모로 pParent로 설정.
if (pParent) // pParent가 있을 경우
{
if (pParent->m_pLeft == pNode) // pParent의 left가 기준 노드일 경우.
pParent->m_pLeft = pLeft; // pParent의 left를 pleft으로 설정.
else // pParent의 right가 기준 노드일 경우.
pParent->m_pRight = pLeft; // pParent의 right를 pleft으로 설정.
}
else // pParent가 없을 경우.
m_pRoot = pLeft; // root를 pLeft로 설정.
pNode->m_pParent = pLeft; // 기준 노드의 부모를 pLeft로 설정.
return pLeft;
}
// 노드의 높이를 구함.
int GetTreeHeight(PNode pNode)
{
if (!pNode) // 노드가 없을 경우.
return 0;
int iLeft = GetTreeHeight(pNode->m_pLeft);
int iRight = GetTreeHeight(pNode->m_pRight);
// 삼항연산자 : 조건식이 true일 경우 ? 뒤의 값이 반환되고 조건식이 false일 경우 : 뒤의 값이 반환됨.
int iFactor = iLeft > iRight ? iLeft : iRight; // left와 right 중 큰 값을 찾아서 저장.
return iFactor + 1; // 저장한 값에 1을 더해서 리턴.
}
// 높이 차이를 구함.
int BalanceFactor(PNode pNode)
{
return GetTreeHeight(pNode->m_pLeft) - GetTreeHeight(pNode->m_pRight);
}
// 트리의 균형을 맞춤.
void ReBalance(PNode pNode)
{
if (!pNode) // 노드가 없을 경우.
return;
int iFactor = BalanceFactor(pNode); // 높이 차이를 구해서 받음.
if (iFactor <= -2) // 오른쪽으로 균형이 무너졌을 경우
{
int iRightFactor = BalanceFactor(pNode->m_pRight); // RR인지 RL인지 판단하기 위해 기준 노드의 right를 넣고 값을 구함.
if (iRightFactor < 0) // -1이 나올 경우 RR.
{
pNode = RotationLeft(pNode); // 기준 노드를 중심으로 좌회전.
}
else // 1일 경우 RL.
{
RotationRight(pNode->m_pRight); // 기준 노드의 right를 중심으로 우회전.
pNode = RotationLeft(pNode); // 기준 노드를 중심으로 좌회전.
}
}
else if (iFactor >= 2) // 왼쪽으로 균형이 무너졌을 경우.
{
int iLeftFactor = BalanceFactor(pNode->m_pLeft); // LL인지 LR인지 판단하기 위해 기준 노드의 left를 넣고 값을 구함.
if (iLeftFactor > 0) // 1이 나올 경우 LL.
{
pNode = RotationRight(pNode); // 기준 노드를 중심으로 우회전.
}
else // -1일 경우 LR.
{
RotationLeft(pNode->m_pLeft); // 기준 노드의 left를 중심으로 좌회전.
pNode = RotationRight(pNode); // 기준 노드를 중심으로 우회전.
}
}
ReBalance(pNode->m_pParent); // 부모노드로 타고들어가며 균형이 무너졌는지를 판단.
}
};main.cpp
#include <iostream>
#include "AVLTree.h"
int main()
{
CAVLTree<int, int> avlTree;
for (int i = 0; i < 20; ++i)
{
avlTree.insert(i + 1, i + 1);
}
CAVLTree<int, int>::iterator iter = avlTree.begin();
CAVLTree<int, int>::iterator iterEnd = avlTree.end();
for (; iter != iterEnd; ++iter)
{
iter->Output();
}
std::cout << "================= erase(12) =================" << std::endl;
avlTree.erase(12);
iter = avlTree.begin();
iterEnd = avlTree.end();
for (; iter != iterEnd; ++iter)
{
iter->Output();
}
std::cout << "================= erase(8) ================="<< std::endl;
avlTree.erase(8);
iter = avlTree.begin();
iterEnd = avlTree.end();
for (; iter != iterEnd; ++iter)
{
iter->Output();
}
return 0;
}
[ 결과 ]
Key : 1 Value : 1
Left : 없음
Right : 없음
Parent : 2
Key : 2 Value : 2
Left : 1
Right : 3
Parent : 4
Key : 3 Value : 3
Left : 없음
Right : 없음
Parent : 2
Key : 4 Value : 4
Left : 2
Right : 6
Parent : 8
Key : 5 Value : 5
Left : 없음
Right : 없음
Parent : 6
Key : 6 Value : 6
Left : 5
Right : 7
Parent : 4
Key : 7 Value : 7
Left : 없음
Right : 없음
Parent : 6
Key : 8 Value : 8
Left : 4
Right : 16
Parent : 없음
Key : 9 Value : 9
Left : 없음
Right : 없음
Parent : 10
Key : 10 Value : 10
Left : 9
Right : 11
Parent : 12
Key : 11 Value : 11
Left : 없음
Right : 없음
Parent : 10
Key : 12 Value : 12
Left : 10
Right : 14
Parent : 16
Key : 13 Value : 13
Left : 없음
Right : 없음
Parent : 14
Key : 14 Value : 14
Left : 13
Right : 15
Parent : 12
Key : 15 Value : 15
Left : 없음
Right : 없음
Parent : 14
Key : 16 Value : 16
Left : 12
Right : 18
Parent : 8
Key : 17 Value : 17
Left : 없음
Right : 없음
Parent : 18
Key : 18 Value : 18
Left : 17
Right : 19
Parent : 16
Key : 19 Value : 19
Left : 없음
Right : 20
Parent : 18
Key : 20 Value : 20
Left : 없음
Right : 없음
Parent : 19
================= erase(12) =================
Key : 1 Value : 1
Left : 없음
Right : 없음
Parent : 2
Key : 2 Value : 2
Left : 1
Right : 3
Parent : 4
Key : 3 Value : 3
Left : 없음
Right : 없음
Parent : 2
Key : 4 Value : 4
Left : 2
Right : 6
Parent : 8
Key : 5 Value : 5
Left : 없음
Right : 없음
Parent : 6
Key : 6 Value : 6
Left : 5
Right : 7
Parent : 4
Key : 7 Value : 7
Left : 없음
Right : 없음
Parent : 6
Key : 8 Value : 8
Left : 4
Right : 16
Parent : 없음
Key : 9 Value : 9
Left : 없음
Right : 없음
Parent : 10
Key : 10 Value : 10
Left : 9
Right : 없음
Parent : 11
Key : 11 Value : 11
Left : 10
Right : 14
Parent : 16
Key : 13 Value : 13
Left : 없음
Right : 없음
Parent : 14
Key : 14 Value : 14
Left : 13
Right : 15
Parent : 11
Key : 15 Value : 15
Left : 없음
Right : 없음
Parent : 14
Key : 16 Value : 16
Left : 11
Right : 18
Parent : 8
Key : 17 Value : 17
Left : 없음
Right : 없음
Parent : 18
Key : 18 Value : 18
Left : 17
Right : 19
Parent : 16
Key : 19 Value : 19
Left : 없음
Right : 20
Parent : 18
Key : 20 Value : 20
Left : 없음
Right : 없음
Parent : 19
================= erase(8) =================
Key : 1 Value : 1
Left : 없음
Right : 없음
Parent : 2
Key : 2 Value : 2
Left : 1
Right : 3
Parent : 4
Key : 3 Value : 3
Left : 없음
Right : 없음
Parent : 2
Key : 4 Value : 4
Left : 2
Right : 6
Parent : 7
Key : 5 Value : 5
Left : 없음
Right : 없음
Parent : 6
Key : 6 Value : 6
Left : 5
Right : 없음
Parent : 4
Key : 7 Value : 7
Left : 4
Right : 16
Parent : 없음
Key : 9 Value : 9
Left : 없음
Right : 없음
Parent : 10
Key : 10 Value : 10
Left : 9
Right : 없음
Parent : 11
Key : 11 Value : 11
Left : 10
Right : 14
Parent : 16
Key : 13 Value : 13
Left : 없음
Right : 없음
Parent : 14
Key : 14 Value : 14
Left : 13
Right : 15
Parent : 11
Key : 15 Value : 15
Left : 없음
Right : 없음
Parent : 14
Key : 16 Value : 16
Left : 11
Right : 18
Parent : 7
Key : 17 Value : 17
Left : 없음
Right : 없음
Parent : 18
Key : 18 Value : 18
Left : 17
Right : 19
Parent : 16
Key : 19 Value : 19
Left : 없음
Right : 20
Parent : 18
Key : 20 Value : 20
Left : 없음
Right : 없음
Parent : 19
[ 설명 ]

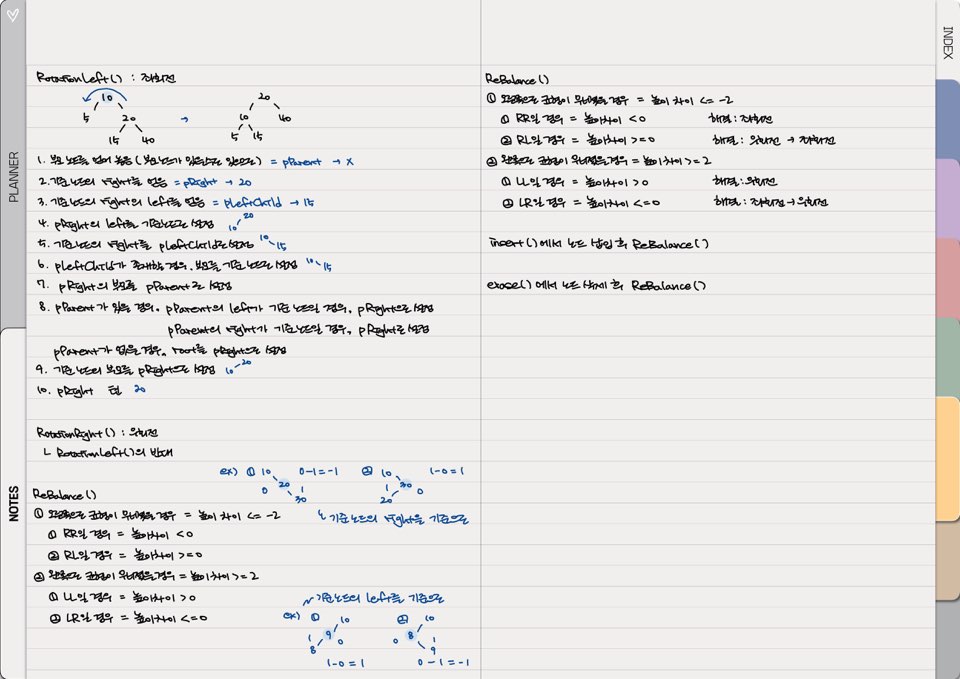

'Study > 자료구조' 카테고리의 다른 글
| [자료구조/정리] 레드 블랙 트리 (0) | 2020.09.22 |
|---|---|
| [자료구조/정리] 이진 탐색 트리(Binary Search Tree) (0) | 2020.09.20 |
| [자료구조/정리] 큐(Queue) (0) | 2020.09.17 |
| [자료구조/정리] 스택(Stack) (0) | 2020.09.17 |
| [자료구조/정리] 배열(Array) (0) | 2020.09.16 |
댓글